|
Özet:
Bu makale, müzisyenler ve bilgisayar mühendisleri için Temel Akustik
ve Sinyal İşleme ile ilgilidir..
Eğer hep kendi kayıtlarını yapmak
ve ya bilgisayarınızda ses ile ilgilenmek istediyseniz, bu makale tam size
göredir.
Tanıtım
Bu makale eğitimi amaçlamaktadır. Okuyucuya temel ses ve ses işleme bilgisini
vermeyi umar.Tabii ki müzik bizim ilgilenmek istediğimiz konulardan biridir ama
diğer az memnun edici sesler arasında sadece bazı gürültüdür.
İlk önce, sesin
fiziksel kavramı, onu insan kulağının işlemesi ile sunulur.Sonra, sinyallere
bakılır.Örneğin Örnekleyiciler veya bilgisayarlar gibi modern dijital araçlarla
ses kayıt edildiğinde nasıl bir şey olur.
En son olarak, mp3 veya Ogg vorbis
gibi güncel sıkıştırma teknikleri sunulur.
Bu makalede anlatılan konu büyük
bir okuyucu kitlesi tarafından anlaşılabilirdir. Yazar, kullanımı zor olan
"normal terminoloji"yi ve müzisyenlerin kullandığı teminolojoyi kullanmayı
denemiştir. Bazı matematiksel formüller ve bazı resimler kullanılmıştır ama
bunları fazla dert etmeyin (uuuu!!!ne rahatlama ama) ...
Birazcık Fizik
Ses
Fiziksel olarak ses, gaz, sıvı veya katı ortamlarda mekanik
titreşimlerdir. Ortamın elastik özelliği sesin kaynaktan dalgalar halinde
uzaklaşmasını sağlar, göle atılan bir taş gibi...
Bir nesnenin her
titreşmesinde, bu nesnenin çevresini saran şeyler içinde sese dönüşerek bir
parça enerji kaybına neden olur.Şu anda diyebiliriz ki vakum oranında ses
yayılmaz.
Şekil 1a, titreşen bir kaynağa bağlı iğnenin, altından bir kağıt
şeridi geçirildiğinde nasıl dalgaya dönüştürdüğünü gösterir.
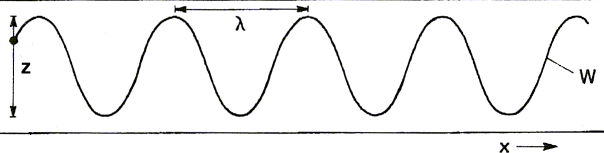
z:±A0 büyüklüğündeki bir titreşen iğne
lamda;: dalga
boyu
x:c hızındaki band hızı
w: Oluşan dalga
Şekil 1a:
Hareket eden bir kağıt şerit üstündeki titreşen
iğne
|
Hava göz önüne alındığında, ses bir basınç çeşidi olarak yayılır.Bir
hoparlör, basınç çeşitlerini çevresindeki havaya iletir.Sıkıştırma (zayıf) hava
içinde yayılır.Burada havanın değil sadece basıncın iletildiğine dikkat
edin. Daha önce bahsedilen su dalgası da, dalga ilerlediği halde su yerinde
kalır.Yüzen nesne sadece yukarı ve aşağı hareket eder.Bu yüzden bir hoparlörün
önünde "rüzgar" oluşmaz. Ses dalgaları 20°C sıcaklıktaki havada yaklaşık saniyede
344 metre hızla ilerler ancak hava parçacıkları sadece birkaç mikron ileri ya da
geri gider.
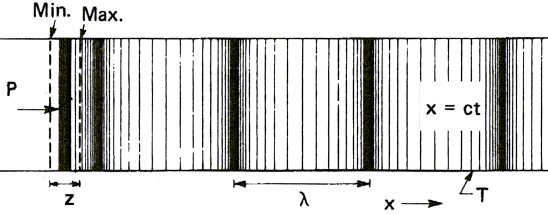
P:
Titreşen piston
T: Tüp
t: zaman
Şekil 1b: sıvı içindeki
titreşen piston
Frekans ve Ses Seviyesi
Yukarıdaki şekillerden anlayacağımız gibi, ses dalgaları sinüs
şeklindedir.İki tepe arasındaki uzaklık dalga boyu olarak adlandırılır ve bir
saniyede gözlenen dalga tepesi sayısına frekans denir.Bu fiziksel terim
müzisyenlerin ses seviyesi dedikleri şey ile aynıdır.Düşük frekansla bas sesler,
yüksek frekanslar ise yüksek seviyeli seslerdir.
Şekil 2, havada ilerleyen
ses dalgasının dalga boyu ve frekans değerlerini vermektedir:

λ: Dalga
boyu
F: Frekans
Şekil 2: Havadaki dalga boyu ve
frekans
Genlik ve Seslilik
Sesin diğer bir karakteristiği ise genliğidir.Sesler yumuşak veya yüksek
olurlar.Bu havada, havayı sıkıştırmak için kullanılan güce bağlı olan küçük veya
büyük basınç çeşididir. Akustikçiler ses gücünü desibel ile ölçerler. Desibel şekil
3a ve 3b'de görüldüğü gibi anlaşılması zor bir birimdir.Bu şekillerin
seçilmesinin sebebi anlaşılmasının kolay olması ve diğer bölümde göreceğimiz
gibi bu logaritmik formül kulağın işleyişine karşılık gelmektedir.Şüphesiz
bilmeden matematik kullanıyorsunuz:
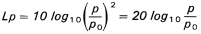 |
|
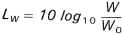 |
| Şekil 3a: Gürültü seviyesi ve basınç |
|
Şekil 3b: Gürültü seviyesi ve
güç |
Şimdiye kadar, dB'nin ses gücüyle ilgili olduğunu bilmemiz yeterlidir.0 dB,
insan kulağının işitebildiği düşük eşit değeridir, gürültünün olamaması
değildir.Desibel, insanın kapasitesine göre gürültü ölçümüdür.Referans
noktasının değişimi (Po ya da Wo) yukarıdaki dB değerlerini
değiştirecektir.Müzik setinizin üzerinde yazan dB değeri akustik seviyeler değil
cihazın elektriksel çıkış gücüdür.Bu tamamen farklı bir ölçümdür. 0 db sıklıkla
amplifikatörün maksimum çıkış gücüdür.Akustik işin içine girdiğinde, dB
cinsinden ses seviyesi çok daha büyük olur.Yoksa bu cihazı almazdınız.Ancak bu
sizin hoparlörünüzün performansına da bağlıdır. Şekil 4, birkaç sıradan ses
kaynağını genlik ve frekans olarak tanımlar.Eğriler, insan kulağının hissettiği
sesliliğin seviyedir.Ayrıntıyı daha sonra anlatacağız:
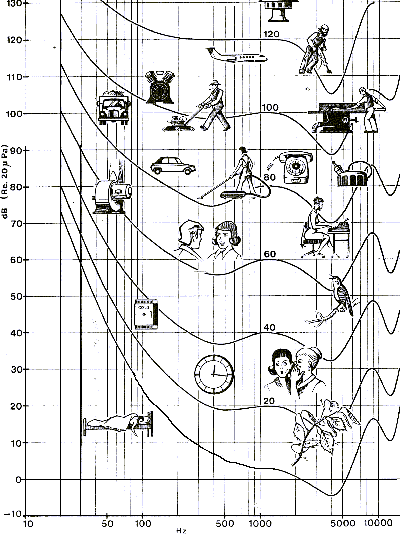
Şekil 4: sıradan ses kaynaklarının
akustik seviyeleri
Aşağıdaki dizi, birkaç sıradan ses kaynağının desibel ve watt cinsinde
seviyelerini verir. Desibelin notasyonu nasıl kolaylaştırdığına dikkat
ediniz:
| Güç (Watt) |
Seviye dB |
Örnek |
Güç (W) |
| 100 000 000 |
200 |
Saturn V Roketi
4 jet motorlu uçak |
50 000 000
50 000 |
| 1 000 000 |
180 |
| 10 000 |
160 |
| 100 |
140 |
Büyük orkestra |
10 |
| 1 |
120 |
Kullanılan çekiç |
1 |
| 0.01 |
100 |
Yüksek sesli bir konuşma |
0.001 |
| 0.000 1 |
80 |
| 0.000 001 |
60 |
Karşılıklı bir konuşma |
20x10-6 |
| 0.000 000 01 |
40 |
|
|
| 0.000 000 000 1 |
20 |
Fısıltı |
10-9 |
| 0.000 000 000 001 |
0 |
|
|
| Tipik ses kaynaklarının ses çıkış
güçleri |
Ses genliği değişik yollardan hesaplanabilir.Bu diğer sinyallere de
uygulanabilir.Şekil 5'te bir örnek verilmiştir:
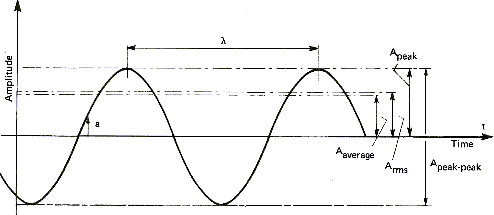
Şekil
5: Sinyal seviyesinin çeşitli ölçümleri
| Sembol |
İsim |
Tanım |
| Aortalama |
Oralama Genlik |
Pozitif sinyalin aritmetik ortalaması |
| ARMS |
Root mean square |
Genliğin enerji içeriğine oranı |
| Atepe |
Tepe Genliği |
Maksimum Pozitif Genlik |
| Atepe-tepe |
Tepeden Tepeye Genlik |
Pozitiften negatife maksimum genlik |
Ortalama genlik sadece teorik bir ölçümdür ve teknik olarak kullanılmaz.Diğer
yönden, root mean square değeri evrensel olarak eşdeğer sinyalleri ölçmek için
kabul edilmiştir (genellikle sinüs dalgaları). Örneğin, Evinizde bulunan
elektrik 220 Volt'a ayarlanmış ve 50 Hz sabitlenmiştir.Burada 220 V RMS
değeridir ve gerçekte voltaj -311 ile 311 V arasında osilasyon yapmaktadır.Diğer
tanımları kullanırsak, bu voltaj 311 V tepe değerine ve 622 V tepeden tepeye
değere sahiptir.Aynı tanım amplifikatörlere de uygulanabilir.10 W RMS değerine
sahip bir amplifikatör 14 W tepe değerine ve 28 W tepeden tepeye değere
sahiptir. Bu tepeden tepeye değer satıcılar tarafında müziksel güç olarak
adlandırılır çünkü satış için güzel bir özelliktir.
Zaman ve Boşluk
Zaman akustikte önemli bir rol oynamaktadır.Zaman ile boşluk arasında önemli
bir bağ vardır çünkü ses bir dalgadır ve zamanla boşluk içinde ilerler.Bunu
hesaba katarsak, üç çeşit akustik sinyal tanımlayabiliriz:
- Periyodik: Sinyaller zamanla tekrarlanır
- Rastgele: Sinyaller periyodik değildir. Aşağıda bu sinyallerin bir bölümü
ile uğraşacağız; zamana bağlı olarak belirli bir düzeni
olanlarla. Müzisyenlerin ve bilim adamlarının beyaz veya pembe gürültü dedikleri
sinyallerdir.
- Darbeler: Sinyaller zamana bağlı olarak tekrarlanmaz ama şekilleri
bellidir.
Şekil 6, bazı ses sinyallerini göstermektedir.Spektrum kavramını açıklamak
için bu diyagramı kullanacağız.Sinyal spektrumları, farklı notaları veya karmaşık
ses sinyallerini oluşturan saf sinyalleri gösteriri.Eğer bir siren veya ıslık
gibi sabit peryodik sinyalleri alırsak, spektrum zamana bağlı olarak sabittir ve
sadece bir değeri gösterir (Şekil 6a'daki tek çizgi). Bunun sebebi, her sesi
aslında sinüs dalgası olan saf sinyallerin bileşimi olarak
düşünebilmemizdir.İleride Fransız matematikçisi Fourier'in 19. yüzyılda ses
sinyallerinin sinüs sinyalleri olarak ifade edilebileceğini gösterdiğini
göreceğiz.Bu bize müzik işin içine girdiğinde, akorddan bahsetme şansı
vermektedir.Aynı zamanda, ben sinüs dalgalarına takıldım çünkü sinüs
dalgalarının çizimi, Jimmy Hendrix'in sololarını çizmekten daha kolaydır.
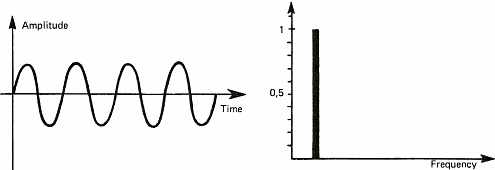
Şekil 6a: Saf sinüs sinyali (basit ve
periyodik)
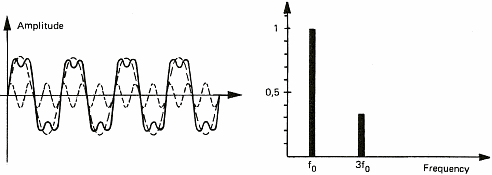
Şekil 6b: İki sinüs sinyalinin birleşimi
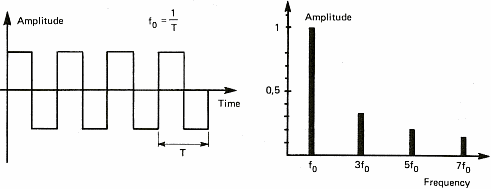
Şekil 6c:
Kare dalga (karmaşık ama periyodik)
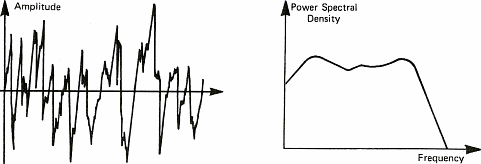
Şekil 6d: Rastgele
sinyal (karmaşık ve peryodik değil)
Şekil 6: Ses sinyalleri
ve spektrumları
Sesi bilgisayar ile işleme, sesi havadaki basınç değişimlerini
bilgisayarın
anlayabileceği sayılara dönüştürmektir.Bunun için bir mikrofon ile basınçtaki
değişimleri elektrik sinyallerine, bir örnekleyici(sampler) ile elektrik
sinyallerini sayılara dönüştürürüz.Örnekleyici genel bir terimdi ve
ADC(Analog to Digital Converter - Analog Dijital Dönüştürücü) elektronik
anlamındaki adıdır. Bu işlemleri bilgisayarlarda ses kartları yapar. Ses kartının
noktaları(numaraları) kaydetme hızına örnekleme frekansı denir. Şekil 7,
örnekleme frekansının ses sinyali ve onun Fourier dönüşümü ile hesaplanmış
spektrumunu nasıl etkilediğini göstermektedir.Matematik meraklıları için formül
aşağıdadır:
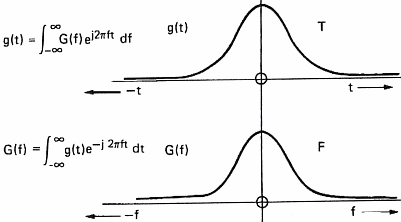
Şekli 7a: İntegral Dönüşümü
Zaman ve frekans alanında
sonsuz ve sürekli
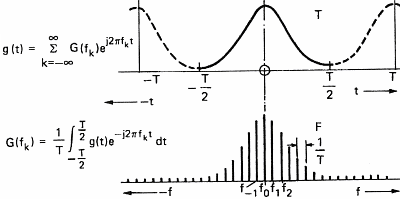
Şekil 7b: Fourier Serileri.
Zaman
içinde periyodik ve freakns alanında ayrık
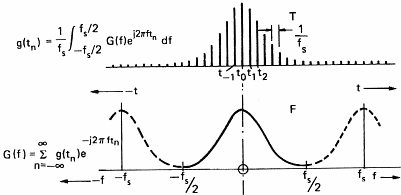
Şekil 7c:
Örneklenmiş Fonksiyonlar.
Zaman içinde ayrık ve frekans alanında
periyodik
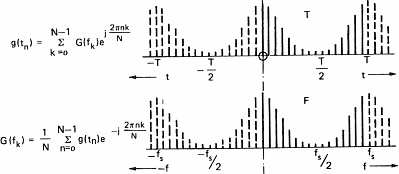
Şekil 7d: Ayrık Fourier Dönüşümü
Hem zman hem
frekans alanında periyodik ve ayrık
Bu (inanın bana), sürekli dalganın ayrık noktalar serisine dönüşümü spektrumu
periyodik yapar. Eğer sinyalde periyodik ise spektrum da ayrık(noktalar serisi)
olur ve sadece sonlu sayıdaki frekans için hesaplamak yeterlidir.Bu iyi bir
haberdir çünkü bilgisayarlar sadece sayıları hesaplayabilirler dalgaları
değil.
Şimdi Şekil 7d'deki durumla karşı karşıyayız. Ses sinyali ve spektrumu
noktalar serisi olarak biliniyor ve bu noktalar zaman ve frekans alanında 0
Hz'den örnekleme frekansının yarısına kadar değişiyor.
Bütün bu şekiller
sonunda orjinal ses biraz kayba uğruyor.Bilgisayar sadece önemli zamanlardaki
sesi biliyor.Bu kaydın çalınabilir ve yeterince iyi olduğundan emin olabilmek
için sesi örneklerken dikkatli olmalıyız.Yapılacak ilk iş, kaydedilecek en büyük
frekansın örnekleme frekansının yarısına küçük olmasına dikkat etmektir.Bu şart
sağlanmazsa yüksek frekanslar daha düşük frekans gibi kaydedilir ve berbat bir
kayıt olur.Bu durum Şekil 8'de gösterilmektedir:
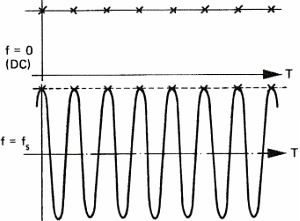
Şekil 8a: Aliasing
Üstteki: Örnekleme frekansı maksimum
frekansa eşittir ve örnekleyici tarafından DC sinyal olarak görünür.
Aşağıda:
fs frekans örneği değerindeki frekans bileşeni DC sinyal gibi
yorumlanır.
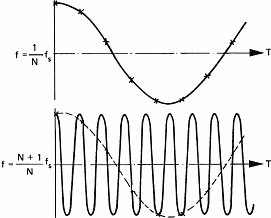
Şekil 8b: Aliasing.
Üstte: (1/N)fs değerindeki
frekans
Aşağıda: [ (N+1)/N ]fs değerindeki frekans bileşeni (1/N)fs olarak
yorumlanır.
-Örneklenmiş sinyali bu belirli davranışı, en iyi Shannon teoremi olarak
bilinir.Shannon, bu olayı açıklayan matematikçidir.Aynı durum genellikle western
filmlerindeki arabaların tekerlerinde de görünür.Bu tekerlerin sanki ters tarafa
dönüyormuş gibi görünmelerinin sebebi, filmlerdeki stroboskobik etkidir.Bunun
anlamı örnekleme frekansının yarısından büyük frekansları elemeniz gerekir.Bunu
yapmazsanız, orjinal ses yanlış seslere bölünür.CD'lerin örnekleme
frekansını(44.1 KHz) ele alalım;22 KHz üzerindeki frekansların yok olması
gerekir ( yarasalarınıza sessiz olmalarını söyleyin çünkü onlar ultra ses ile
konuşurlar.).
İstenmeye frekanslardan kurtulmak için süzgeçler kullanılır.Süzgeçler, sesin
bir kısmını ileten veya koruyan cihazlardır.Örneğin alçak geçiren süzgeçler,
duyulmaya ancak örneklemeyi bozan yüksek frekansları (yarasaların
fısıltıları) geçirmez.Daha fazla detaya girmeden süzgeçlerin
karakteristiklerini gösteren şekler bir göz atalım:
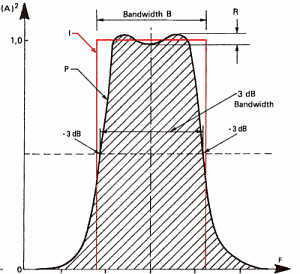
Şekil 9: Prtaikte süzgeç ve ideal süzgeç
I: İdeal
süzgeç
P: Pratikteki süzgeçr
R: Ripple
B: Etkin bad genişliği
Süzgeç, sinyallerin hem zamanını hem de spektrumunu değiştiren cihazdır.200
Hz'de alçak geçiren filtreden geçen 100 Hz'lik kare dalga, sinüz sinyali olur
çünkü spektrumunun üst kısmı yok olur.Benzer şekilde, 1000 Hz'lik bir piyano
notası 1200 ya da 1500 Hz'lik filtreden geçtiğinde, fısıltı gibi duyulur.Bir
sesin en alçak frekansı, temel frekans olarak adlandırılır.Diğerleri bileşendir
ve harmonik frekanslar olarak adlandırılırlar.
Zaman alanında, süzgeçler,
bozulma(distorsiyon) adı verilen değişikliklere neden olurlar.Bunun temel nedeni
harmonikler arasındaki zaman farklarıdır.
Bir süzgecin bir sinyal üzerindeki etkisini görebilmek için basit bir kare
dalgana (şekil 10a), spektrumunun genliğine(şekil 10b), spektrumunun
fazına(şekil 10c) bakalım.Bu kare dalga, bir süzgeç gibi t=0'dan t=T anına kadar
sesi geçirir.Bu darbenin spektrumu, süzgeçin frekans tepkisini
gösterir.Gördüğümüz gibi sinyal frekansı ne kadar büyükse frekans bileşenleri
arasındaki zaman farkı o kadar büyük olur ve genlik de o kadar küçük olur.
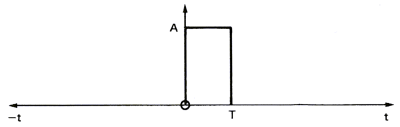
Şekil 10a: Zaman sinyali. t=0 anındaki dikdörtgensel
darbe
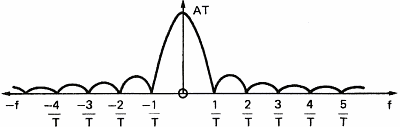
Şekil 10b: Sektrum (Genlik)
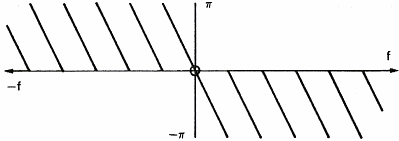
Şekil 10c: Spektrum
(Faz).
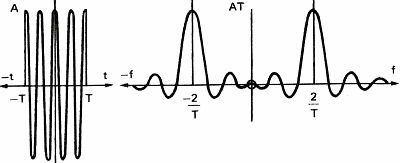
Şekil 11, dikdörtgensel süzgecin sinüs sinyali gibi basit bir sinyal
üzerindeki etkilerini göstermektedir.
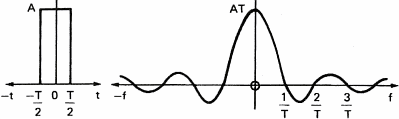
Şekil 11a: Dikdörtgensel darbe.
t=0 anındaki
darbe.
Şekil 11b: Ses darbesi.
Sesi T anında aniden keseme, sinüs dalgasının spektrumunda yeni frekansları
oluşturur.Eğer süzülmüş sinyal, fazla karışık(şekil 6c'deki kare dalga gibi) ise
frekans bileşenleri, süzgecin çıkışında bozukmuş sinyaller oluşturur.
Fiziko-akustik
İnsan Kulağı
Akustiği ve sesi daha iyi anlamak için, sesi duyduğumuz organımıza
odaklanalım:Kulak
Şekil 12, kulağın enine kesitini görebilirsiniz.Ses,
pinna'da toplanır ve az çok mikrofon gibi çalışan kulak zarına doğru
yönlendirilir.Kulak zarının titreşimleri, itme-çekme şeklinde çalışan üç küçük
kemik yardımıyla yükseltilir.Bu kemiklerin adı çekiç, örs ve üzengidir.
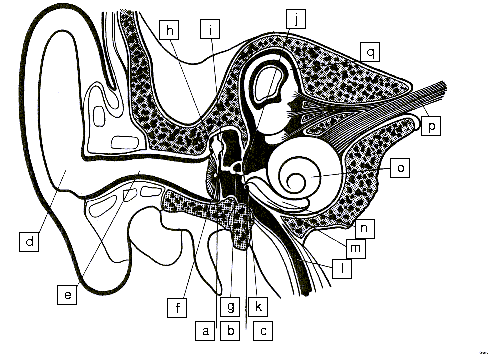 |
|
a) Dış kulak
b) Orta kulak
c) İç kulak
d) Pinna
e) Kulak
kanalı
f) Kulak zarı
g) Stapes
h) Malleus
i) Incus
j) Oval
Pencere
k) Yuvarlak Pencere
l) Eustachian Tube
m) Scala
Tympani
n) Scala vestibuli
o) Cochlea
p) Sinir Fiberi
q)
Yarımdaire kanalı
|
| Şekil 12: Kulağın ana
parçaları |
Üzenginin hareketleri, oval pencere aracılığıyla cochlea'ya iletilir. Cochlea,
basilar zar ile ayrılmış iki odadan oluşur.Bu zar işitme sinirlerine bağlı
hassas kıl hücreleri ile kaplanmıştır(Şekil 13 ve 14'de görülebilir). Basilar
zar, bir süzgeç gibidir çünkü cochlea'nın çeşitli yerleri çeşitli frekanslara
hassastır. Böylece beyin notaları ayırt edebilir.
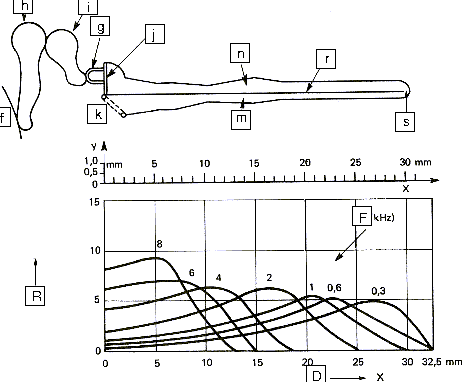 |
|
f) Kulak Zarı
g) Üzengi
h) Çekiç
i) Örs
j) Oval
Pencere
k) Yuvarlak Pencere
m) Scala Tympani
n) Scala
vestibuli
r) Basilar Zar
s) Helicotrema
R) Bağlı Cevap
F)
Frekans Cevabı
D) Zar boyunca uzaklık
|
| Şekil 13: Cochlea'nın Boyuna
Kesiti |
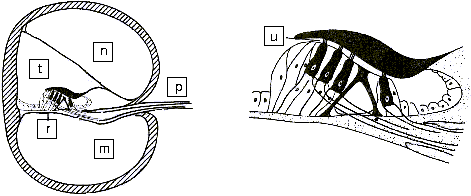 |
|
m) Scala Tympani
n) Scala vestibuli
p) İşitme Siniri
r)
Basilar Zar
t) Scala media
u) Kıl Hücresil
|
| Şekil 14: Cochlea'nın yatay
kesiti |
Algılama
Beyin çok önemli bir rol oynamaktadır çünkü beyin, sesi tanıma -ses
seviyesine göre ve sesin süresine göre- için bütün analizleri yapar.Beyin,
ayrıca sesin yerini tayin etmek için iki kulaktan gelen bilgileri
birleştirir.Böylece sesin, hangi müzik aletine veya kişiye ait olduğunu ve
yerini anlayabiliriz. Beynin yaptığı bütün işler sonradan öğrenilmiştir.
Şekil
15, frekanslara göre nasıl duyduğumuzu göstermektedir..
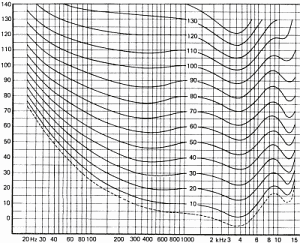
Şekil
15: Eşit seslilik sınıları
Yukarıdaki eğriler, ortalama bir popülasyon için çizilmiştir ve saf tonlar
için 18-25 yaş grubundan insanlar tarafından oluşturulmuş bir istatistiksel
sonuçtur.Aşağıdaki sebepler nedeniyle kişiden kişiye değişebilmektedir:
- tecrübe: örneğin müzisyen olmak ya da olmamak.
- gürültüye maruz kalma.
- yaş.
- ...
Şekil 16, yaşın duyma kaybı üzerindeki etkisini değişik frekanslar için
göstermektedir.Kaynaklara göre sonuç da faklı olmaktadır.Bu, bir popülasyon
içinde gözlenen çeşitlilik ile kolayca açıklanabilir çünkü bu çalışmalar sadece
yaşı kolayca hesaba katamazlar.Yaşlı ama genç kulaklara sahip müzisyen az
rastlanır bir durum değildi.Aynı şekilde, genç ancak konserler veya gece
klüpleri gibi yüksek sese uzun süre maruz kaldıklarından dolayı duyma kaybı olan
kişiler de oldukça fazladır.
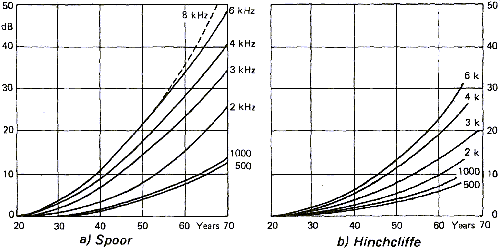
Şekil
16: Spoor ve Hinchcliffe'ye göre yaş ile duyma kaybı ilişkisi
Gürültünün duyma kaybına neden olması, maruz kalma süresine ve gürültünün
yoğunluğuna bağlıdır.Burada sadece rahatsızlık verici seslere değil bütün
seslere gürültü denmektedir.Kulaklık ile yüksek sesli müzik dinleme ile konmakta
olan bir uçağı dinlek, işitme hücreleri üzerinde aynı etkiye sahiptir.
Şekil
17, gürültüye maruz kalmanın duyma üzerindeki etkisini göstermektedir.Etkinin,
kulakların yüksek frekanslara karşı hassaslığını kaybettiği yaşlarla aynı
şekilde etkilenmediğine dikkat ediniz.Diğer taraftan, duyma kaybına neden olan
gürültü, 3-4 Khz'ler civarında frekans hassasiyetini azaltır.Bu frekanslar,
kulağın en hassas olduğu frekanslardır.Bu tür duyma kayıpları genelde silah
kullananlarda görünür.
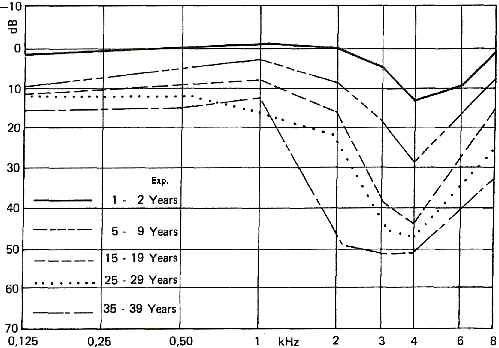
Şekil
17: Duyma kaybına neden olan gürültünün gelişimi
Exp.: Maruz kalma
yılları
Eğer desibel ve desibel ölçümlerinin anlatıldığı bölüme bakarsanız, 10
desibel civarının çok büyük akustik basınç değişiminin olduğunu
görürsünüz.Lineer bir desibel skalası, eksponansiyel bir basınç skalasına denk
gelir. Bu yüzden kulaklar ve beyin, gemlikte ve frekansta çok büyük değişimlerle
uğraşmak zorunda kalır. İnsan kulağını duyabildiği en yüksek frekans, duyabildiği
en küçük frenaksın 1000 katıdır. Duyabildiğin en yüksek ses, duyabildiği en küçük
sesin bir milyar katıdır (yoğunluk oranı, 1'e 1012'dir).
Basıncı
ikiye katlamak sadece 3dB'lik bir değişimi ifade eder. Bu duyulabilir ama sesin
yoğunluğundaki 9 dB'lik bir atış, insan kulağı için sesin iki katına çıkması
demektir.Bu akustik basıncın 8 kat daha fazla olması demektir.
Frekans
alanında, oktavın değişimi, frekansın iki kat artması demektir.Burada da,
fiziksel olayın eksponansiyel artımı lineer olarak duyulur.Hemen hesap
makinelerine sarılmayacağız, notaların ses seviyelerini daha sonra
hesaplayacağız.
Kayıt
Ses kayıtlarının teyp kaydediciler ile veya vinil disklerle yapılması, dijital
sistemlerin olmasına karşın hala yaygındır. Her iki durumda da, sesin manyetik osilasyon şekline veya dijital veriye
dönüştürülmesi, kayıt cihazına göre bazı
sınırları beraberinde getirir.Daha önceden, örneklemenin, ses spektrumu
üzerindeki etkilerini konuşmuştuk.Diğer etkiler kayıt sırasına
beklenmektedir:
Dinamik aralık
"Dinamik", kayıt cihazının kaydedebildiği en küçük ve en büyük genliği temsil
eder.Genellikle mikrofon ile başlar, sesi elektrik sinyaline dönüştürür, kayıt
ortamına (disk, teyp, bilgisayar) gider.
Oranları belirleyen desibelleri
hatırlayın.Dinamik aralık düşünüldüğünde, bu değer, en küçük değer olan 0 dB'e
karşılık gelir.Birkaç örnek verelim:
- Vinil disk: 65 dB
- Manyetik tape: 55 dB
- 16 bit örnekleme (CD): 96 dB
- 8 bit örnekleme: 48 dB
Bir semfoni orkestrası, 110 dB'lik bir aralıkta çalabilir.Bu yüzden, disk
editörleri, sıkıştırma sistemleri kullanır.Böylece çok yüksek sesler kırpılmaz
ve küçük sesler yok olmaz.
Ground Gürültüler
İnsan kulağından daha yeteneksiz olmalarına ek olarak, kayıt cihazlarının
zorluk çıkarakn yanları, kendi gürültülerini çıkarmalarıdır.Bunun sebebi,
elmasın vinil disk üzerinde kayması veya amplifikatörün kendi hırıltısıdır.Bu
tür gürültüler çok küçüktür ancak alçak seslerin kaydedilmesini engeller.En iyi
kaliteli bir kulaklık ile şelale gibi bir ses olarak duyulur.Çünkü geniş bir
frekans spektrumu vardır.
Bozulma
Daha önce de gördüğümüz gibi süzgeçlerin spektrum fazı üzerinde önemli bir
etkisi varır.Çünkü sinyalleri, frekansına göre kaydırırlar.Bu tür bozulmalara,
harmonik bozulma denir.Çünkü sinyallerin harmonik frekanslarını etkiler.
Her
ses kaydeden cihaz, bir süzgeç olarak davranır ve böylece bozulmalara neden
olur.Tabii ki bu, kaydedilmiş her sinyali dinlerken de olur.Fazladan gürültü ve
bozulma eklenir.
Sıkıştırma
Bu algoritmaların yıkıcı oldukları söylenebilir çünkü bu algoritmalar sesin
bazı kısımlarını yer açmak için yok eder.Sesin duyulmayan kısımları yok etmek
için sıkıştırma algoritmaları, insan kulağının bilgisayar modelini
kullanır.Örneğin, Birbirine yakın iki frekans varsa bunlarda az duyulanını
atabilirsiniz çünkü baskın olan diğerini maskeleyecektir.Bu yüzden bazı testler
ve tavsiyeler, bu algoritmaların en iyi kullanımı için internette
yayınlanmaktadır.Çoğu mp3 sıkıştırması, 16 KHz'de alçak geçiren süzgeç olarak
çalışır ve 128 KiloBit/saniye'den daha yüksek hızlara izin vermez.Bu, çoğu zaman
CD kalitesinin yakalanamaması demektir.
Diğer taraftan, gzip, bzip2, lha veya
zip verileri değiştirmez ancak daha az sıkıştırma sağlar.Dahası, bütün kaydı
dinleyebilmek için önce sıkıştırılmış veriyi açmak gerekir.Bu bir walkman ya da
başka dinleme cihazları için istenilen bir şey değildir.
Peki ya müzik?
Kavramların oturması için, müzisyenler ve bilim adamları tarafından kullanılan
terimleri karşılaştıralım.Çoğu zaman, karşılaştırmalar sınırlıdır çünkü
müzikseverlerin kullandıkları terimler insan kulağı ile ilgidir, fiziksel
olaylarla değil.
Notalar ve saf frekanslar
Bir nota, diğerleri arasında, kendi ses seviyesi olarak
tanımların ve bu ses
seviyesi notanın temel frekansı olarak düşünülebilir.Bunu bilerek, notaları
frekansları, aşağıdaki formülle hesaplanabilir:
FREKANS (hertz olarak)= REFERANS × 2( (OKTAV - 4) + ( TON - 10)
/ 12 )
B>REFARANS olarak 440 Hz'deki 4. oktavdan A notasını kullanırsak,
diğerlerini 1'den 12'ye kadar (C'den B'ye kadar) hesaplayabiliriz:
| Nota |
Oktav |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| C |
32,70 |
65,41 |
130,8 |
261,6 |
523,3 |
1047 |
2093 |
4186 |
| C # |
34,65 |
69,30 |
138,6 |
277,2 |
554,4 |
1109 |
2217 |
4435 |
| D |
36,71 |
73,42 |
146,8 |
293,7 |
587,3 |
1175 |
2349 |
4699 |
| E b |
38,89 |
77,78 |
155,6 |
311,1 |
622,3 |
1245 |
2489 |
4978 |
| E |
41,20 |
82,41 |
164,8 |
329,6 |
659,3 |
1319 |
2637 |
5274 |
| F |
43,65 |
87,31 |
174,6 |
349,2 |
698,5 |
1397 |
2794 |
5588 |
| F # |
46,25 |
92,50 |
185,0 |
370,0 |
740,0 |
1480 |
2960 |
5920 |
| G |
49,00 |
98,00 |
196,0 |
392,0 |
784,0 |
1568 |
3136 |
6272 |
| A b |
51,91 |
103,8 |
207,6 |
415,3 |
830,6 |
1661 |
3322 |
6645 |
| A |
55,00 |
110,0 |
220,0 |
440,0 |
880,0 |
1760 |
3520 |
7040 |
| B b |
58,27 |
116,5 |
233,1 |
466,2 |
932,3 |
1865 |
3729 |
7459 |
| B |
61,74 |
123,5 |
246,9 |
493,9 |
987,8 |
1976 |
3951 |
7902 |
Gerçek müzikseverler, diatonik ve chromatic arasında bir ayrım yapmadığımızı
fark edeceklerdir.Küçük bir değişiklikle, aynı hesap, yarım tonlar yerine
alt bölümler olarak virgülleri kullanarak yapılabilir.
Notaların frekans
olduğunu düşünmek, bir notanın bir aletten diğerine nasıl değiştiğini
açıklamaktan uzaklaşırız.Aynı zamanda, notanın nasıl çalındığını(pizzicato yada
legato), hangi alette çalındığını, glissando, vibrato gibi efektleri hesaba
katmalıyız.Bunun için, notalar, zamana karşı spektrum olan sonogram yardımıyla
incelenebilirler.Sonogram, zaman karşı bütün harmonik frekansların görünmesini
sağlar.
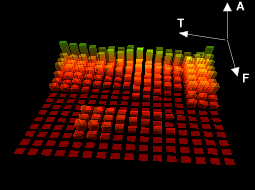
| Şekil 18: Bir sonogram |
| T: Zaman |
A: Genlik |
F: Frekans |
Bugünlerde, elektronik ses kayıt ve çalma cihazları, ses oluşturmak için
sentezleyiciler(synthesizers) veya ses depolayan ve değişik ses seviyelerinde
çalan örnekleyiciler gibi tamamen yapay cihazlar kullanmaktadırlar. Örneklenmiş
sandalye gıcırtısından bir çello konseri vermek mümkündür.Bunu herkes yapabilir
ve bir enstrüman çalabiliyor olmanız gerekmemektedir.Tek bir notanın
karakteristiği aşağıdaki şekilde verilmiştir:
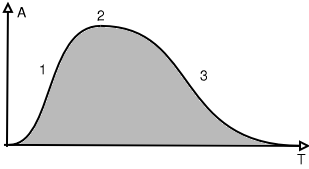
| Şekil 19: Bir notanın karakteristiği: Zarf |
| 1: Yükselme |
A: Pozitif Genlik |
| 2: Durma |
T: Zaman |
| 3: Kaybolma |
|
Eğri, sesin zamana karşı küresel sesliliğinin evrimini gösterir.Bu tip
eğrilere zarf denir çünkü sinyal(şeklin gri parçası) tamamen
paketleniyor.Yükselen kısmına yükselme denir ve enstrümana bağlı olarak birçok
değişik şekilde olabilir.İkinci kısım durma denir ve notanın asıl
kısmıdır.Perküsyon enstrümanları dışındakiler için en uzun süren kısımdır.Üçüncü
kısım, enstrümana göre şeklini ve uzunluğunu değiştirebilir.
Enstrümanlar,
müzisyenlerin bu üç kısmı istedikleri gibi değiştirme şansı vermektedir. Piyanonun
tuşların farklı hızlarda basmak, notanın yükselme alanını, pedallar ise kaybolma
alanını etkiler. Her üç kısım da ses çeşitliliğini sonsuz yapan kendi
spektrumuna(rengine) sahiptir.Harmonik frekanslar, yanı seviyede değişmezler.Bas
frekanslar daha uzun sürmek isterler ve sesin rengi başlangıcında ve sonunda
aynı olmaz.
Aralık
Tanıma göre, bir cihazı frekans aralığı, enstrümanın frekans aralığıyla
ilintilidir.Her iki durumda da terimler, bir enstrümanın çalabileceği frekans
veya ses seviyesi aralığını tanımlar.Bununla birlikte, enstrümanın çalabileceği
en yüksek frekans, yukarıdaki dizide verilmiş olan temel frekansa eşittir.Yani,
eğer sesin bütün renklerini kaydedebilmek için enstrümanın çalabileceği en yüksek
frekanstan daha yüksek frekansları kaydedebilen bir cihaz olmalı.Kısa bir
frekans aralığı, bir alçak geçiren süzgeç olarak işlev görür ve yüksek frekans
harmonilerini kaydetmez. Bu da sesin dolgunluğunu(sonority) yok eder.Pratikte,
insan kulağının duyabildiği frekans aralığına(20Hz - 20KHz) sahip cihazlar
gerekir.Genellik 20 Khz'in üstüne çıkmalıdır çünkü cihazlar kesme(cut off)
frekansının altında sesi bozarlar.
Harmonikler ve Nota Bütünleri
Yukarıdaki notaların frekans dizisini analiz edersek, müzisyenler harmonik
frekanslar arasında bazı benzerlikler ve nota bütünü oluşturan notaları
bulurlar.
Harmonik frekanslar, temel frekansların çeşitlerin içerir.Böylece,
32,7 Hz'deki C notası için harmonik frekanslar aşağıdaki gibi olur:
| Harmonik |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| Frekans |
32,7 |
65,4 |
98,1 |
130,8 |
163.5 |
196,2 |
228,9 |
261,6 |
| Nota |
C |
C |
G |
C |
E |
G |
B b |
C |
Burada bir nota bütünün neden mükemmel (C-E-G-C) ya da yedinci (C-E-G-Bb)
olarak bilindiğini görüyoruz:Nota bütünü içindeki notaların frekansları , temel
(C notasının) frekansının harmonikleri olarak dizilmişlerdir. İşte sihir
buradadır.
Sonuç
Daha fazla detaya inmeden, sesi ve akustiği, fizik, insan açısından ve teknik
açıdan inceledik.En iyi kriterin kulağınız olduğunu söylemeliyiz. Bazı
matematiksel formüller ve ölçme cihazlar, neden bazı kaydedilmiş seslerin garip
olduğunu anlamamıza yardımcı oluyor fakat 60'larda Beatles'ın mı yoksa Rolling
Stones'un mu daha iyi müzik yaptığını açıklayamazlar.
Bibliyografi
Brüel & Kjaer: , akustik ve titreşim
ölçüm cihazları yapan bir Danimarkalı şirkettir.Şirket, elliyldan fazladır
içinde bu makalede de yayınlanan şekilleri içeren ücretsiz kitaplar
yayınlamaktadır.Bu kitapları PDF formatında şu adresten bulabilirsiniz:
http://www.bksv.com/bksv/2148.htm
|



